Geometric Thinking and the Geometry of Conics and Quadrics
This is a “show-and-tell” of what I think should be essential exposure to geometry for engineering students. It is difficult to compose a short article or a long talk that leaves a compelling impression in this regard upon a group as diverse as membership of the International Society for Geometry and Graphics. Therefore an unconventional, possibly misguided, approach will be adopted. I will jump right in with a rambling tale, pictures and equations. These begin with the hyperboloid of one sheet swept by a line that remains intersecting three given ones. This provides opportunity to introduce line geometry, symmetry underlying the three lines and a solution that contains a product of the surface scalar equation in point coordinates along with other factors and their significance. Relevance of eigenvalues and eigenvectors, intersection with the absolute plane and the asymptotic cone are discussed. Can all surfaces of second order be ruled with lines?
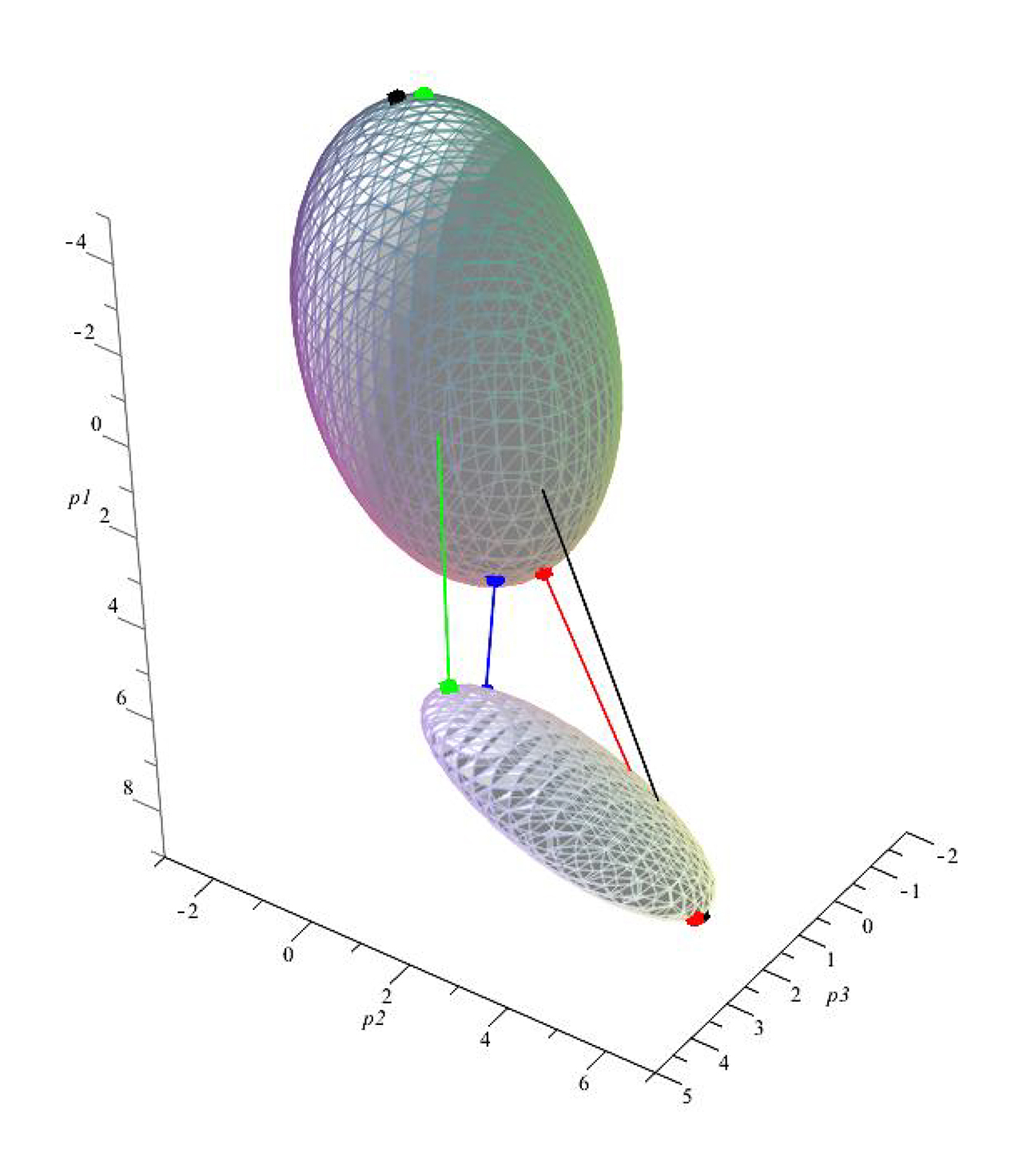
Maybe. This is followed by the second part of my tale that pertains to stationary distances between conics and quadrics; shortest, greatest and inflective. Using Groebner bases, which are truly worthy of a little digression, I show that a pair of conics (ellipses) can have up to 12 such real distances but the univariate solution monomial is of degree 16. I cannot explain significance of those four inevitably complex roots nor can I formulate the problem with four necessary constraint equations so as to obtain a univariate polynomial (UVP) of degree 12.
Taking an example of two ellipsoids Buchberger’s algorithm returns a UVP of degree of 24 and hence we have done better because, given the model of two ellipses, it is easy to see 12 real solutions in Euclidean space and the intersection of the absolute conic pair nicely accounts for another 12. In conclusion and in agreement with Lewis Carol’s four (ambition, distraction, and uglification and derision) I leave you with my four mathematical principles of extension, projection, duality and symmetry. Like a four-legged stool it may wobble a bit if the surface isn’t flat.
To those who may wallow in the confusion I’ve wrought and disagree I’ll just say that geometric thinking contemplates a holographic shard that contains all information in detail however sketchy while analysis is like Ariadne’s yarn leaving Theseus to wonder
as we may do without geometry. Are other ways to the Minotaur?